Bihar Board 10th Math Model Paper 2025 परीक्षा की तैयारी कर रहे सभी छात्रों के लिए गणित विषय का मॉडल पेपर 2025 परीक्षा (math model paper 2025)के लिए Mantu Sir (DLS Education) ले के आ चुके है बिलकुल फ्री मे गणित ऑब्जेक्टिव प्रश्न (math Objective question) बनाने मे काफी मदद मिलेगा आप को बता दे की बिहार बोर्ड 10वी परीक्षा 2025 मे 50 अंक का ऑब्जेक्टिव प्रश्न पूछे जाते है जिस का उत्तर आप को OMR Sheet पर देना होता है महत्वपूर्ण ऑब्जेक्टिव प्रश्न गणित (Math Important Objective Question model paper)के सभी चैप्टर से चुन कर निकाले गए है अब आप बिहार बोर्ड गणित परीक्षा 2025 (Bihar board 10th exam 2025) के लिए आप को तैयारी मे मदद मिलेगा इस सैंपल मॉडल पेपर(sample model paper) के मदद से आप को परीक्षा मे आच्छे अंक लेन मे मदद मिलेगा
Bihar Board 10th Math Model Paper 2025
बिहार बोर्ड गणित मॉडल पेपर 2025(bihar board model paper 2025) गणित मॉडल पेपर मे सभी चैप्टर से जैसे त्रिभुज, त्रिकोणमिती से परिचय,द्विघात समीकरण, वास्तविक संख्याएं से सिर्फ महत्वपूर्ण ऑब्जेक्टिव प्रश्न निकले गए है इस गणित के मॉडल पेपर सेट 3 ( Math Model Paper Set 3) के मदद से आप को गणित के परीक्षा मे पूछे जाने वाले प्रश्न की जानकारी मिल जाएगी और प्रश्न के पैटर्न की भी जानकारी मिल जाएगी आप के लिए बिलकुल फ्री मे Mantu Sir ने ये प्रैक्टिस मॉडल पेपर (Practice Model Paper 2025) तैयार किया है इस मॉडल पेपर के मदद से आप को परीक्षा मे आच्छे अंक लेन मे काफी मदद मिलेगी आप को 10 -20 अंक का वस्तुनिष्ठ प्रश्न इस मॉडल पेपर से सीधा पूछ लिया जा सकता है
Class 10th Objective Question Mock Paper 3
1. \(\frac{92}{115}\) का सरलतम रूप है –
2. दो परिमेय संख्याओं के बीच अधिकतम कितनी परिमेय संख्या हो सकती हैं ?
3. निम्नलिखित में किसका दशमलव प्रसार सांंत है ?
4. बहुपद \(dy^2 + by + a\) के शून्यकों का गुणनफल होगा –
5. \(\sqrt{18}\) का परिमेयकरण गुणांक है –
6. सबसे छोटी अभाज्य संख्या है –
7. यदि \(a = bq + r\), जहाँ \(a\) और \(b\) धनात्मक पूर्णांक हों, तो –
8. निम्नलिखित में कौन परिमेय संख्या है ?
9. द्विघात बहुपद \(x^2 + 12x + 35\) के शून्यक हैं –
10. निम्नलिखित में कौन अपरिमेय संख्या है ?
11. बहुपद \(5y^2 – 25\) के शून्यक हैं –
12. एक द्विघाती बहुपद के शून्यकों का योग तथा गुणनफल क्रमशः 3 तथा \(-40\) हैं, तो द्विघाती बहुपद है –
13. युग्म समीकरण \(x + 2y = 4\) तथा \(2x + 4y = 8\) का है –
14. यदि बहुपद \(x^2 + ax – b\) के शून्यक एक-दूसरे के व्युत्क्रम हों, तो \(b\) का मान होगा –
15. अर्धवृत्त का कोण होता है –
16. द्विघात समीकरण \(ax^2 + bx + c = 0\), जहाँ \(a \ne 0\), के वास्तविक मूल नहीं है यदि
17. यदि \(\alpha\) तथा \(\beta\) समीकरण \(2x^2 – x – 6 = 0\) के मूल हों, तो \(\left(\frac{1}{\alpha} + \frac{1}{\beta}\right)\) बराबर है
A) 6 B) -6 C) \(\frac{1}{6}\) D) \(-\frac{1}{6}\) उत्तर देखें18. समांतर श्रेणी: \(-3, 4, 11, 18, \ldots\) का 21वाँ पद है –
A) 143 B) -143 C) 127 D) 137 उत्तर देखें19. निम्नलिखित में से कौन-सा द्विघात समीकरण है?
A) \(x^3 – x^2 = (x – 1)^3\) B) \(x^2 – 4\sqrt{x} + 14 = 0\) C) \(x + \frac{1}{x} = x^2\) D) \(x^2 + \frac{1}{x^2} = 5\) उत्तर देखें20. समांतर श्रेणी \(80, 76, 72, 68, \ldots\) का कौन-सा पद \(0\) है?
A) 20वाँ B) 21वाँ C) 22वाँ D) 23वाँ उत्तर देखें21. यदि समांतर श्रेणी का सामान्य पद \(6 – 4n\) है, तो इसका सार्व-अंतर होगा –
A) 6 B) 4 C) -4 D) 2 उत्तर देखें22. निम्नलिखित में कौन समांतर श्रेणी है?
A) -2, 4, -6, 8, ……. B) \(a, a^2, a^3, a^4, …….\) C) \(\frac{3}{2}, \frac{1}{2}, -\frac{1}{2}, -\frac{3}{2}, …….\) D) 1, 3, 9, 27, ……. उत्तर देखें23. मूल बिन्दु के नियामक हैं –
A) (-1, -1) B) (1, 1) C) (-1, 0) D) (0, 0) उत्तर देखें24. यदि \(\triangle ABC \sim \triangle PQR\) तथा \(\frac{QR}{BC} = \frac{2}{3}\) तो \(\frac{\text{area of } \triangle PQR}{\text{area of } \triangle ABC} =\)
A) \(\frac{4}{9}\) B) \(\frac{2}{3}\) C) \(\frac{9}{4}\) D) \(\frac{3}{2}\) उत्तर देखें25. दी गई आकृति में \(x\) का मान है
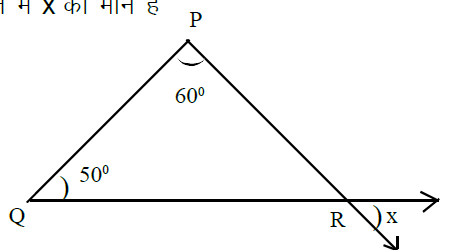 A) 110°
B) 60°
C) 70°
D) 35°
उत्तर देखें
A) 110°
B) 60°
C) 70°
D) 35°
उत्तर देखें
26. बिन्दुओं \(R(0, 6)\) तथा \(S(8, 0)\) को मिलाने वाली रेखाखंड के मध्य-बिन्दु के नियामक हैं –
A) (0, 0) B) (0, 8) C) (8, 16) D) (4, 3) उत्तर देखें27. बिन्दुओं (4, 6) और (8, 2) के बीच की दूरी है –
A) \( 4\sqrt{2} \) इकाई B) \( 6\sqrt{2} \) इकाई C) \( 8\sqrt{2} \) इकाई D) \( \sqrt{2} \) इकाई उत्तर देखें28. \(\sin^2 60^\circ + \cos^2 60^\circ =\)
A) 2 B) 3 C) 1 D) 0 उत्तर देखें29. यदि रैखिक समीकरणों का युग्म संगत हो, तो रेखाएँ होंगी –
A) हमेशा संपाती B) समान्तर C) हमेशा प्रतिच्छेदी D) प्रतिच्छेदी या संपाती उत्तर देखें30. बिन्दु \((-6, -\frac{5}{2})\) किस पाद में स्थित है?
A) प्रथम B) द्वितीय C) तृतीय D) चतुर्थ उत्तर देखें31. \(\triangle PQR\) में भुजा \(QR\) को बिन्दु \(S\) तक इस प्रकार बढ़ाया गया है कि \(\angle PRS = 120^\circ\) और \(\angle QPR = 63^\circ\) तो \(\angle PQR =\)
A) 63° B) 57° C) 60° D) 67° उत्तर देखें32. यदि किसी त्रिभुज के कोण का समद्विभाजक विपरीत भुजा को समद्विभाजित करता है, तो त्रिभुज होगा –
A) समद्विबाहु B) समबाहु C) विषमबाहु D) समकोण उत्तर देखें33. \(\triangle ABC\) में \(DE \parallel BC\) तथा \(\frac{AD}{DB} = \frac{2}{3}\) तो \(\frac{AE}{EC}\) का मान होगा –
A) \(\frac{3}{5}\) B) \(\frac{2}{3}\) C) \(\frac{3}{2}\) D) \(\frac{2}{5}\) उत्तर देखें34. यदि त्रिभुज \(ABC\) तथा \(DEF\) में \(\frac{AB}{DE} = \frac{BC}{FD}\) तो ये समरूप होंगे जब –
A) \(\angle A = \angle F\) B) \(\angle B = \angle E\) C) \(\angle B = \angle D\) D) \(\angle A = \angle D\) उत्तर देखें35. दी गई आकृति में \(PQ\), \(O\) केंद्र वाले वृत्त की स्पर्श रेखा है। यदि \(OQ = 3\) सेमी, \(PQ = 4\) सेमी तो \(OP =\)
 A) 4 सेमी
B) 6 सेमी
C) 5 सेमी
D) 7 सेमी
उत्तर देखें
A) 4 सेमी
B) 6 सेमी
C) 5 सेमी
D) 7 सेमी
उत्तर देखें
36. \(x\)-अक्ष से बिन्दु \(P(8, 12)\) की दूरी है –
A) 8 इकाई B) 12 इकाई C) 20 इकाई D) \(\sqrt{208}\) इकाई उत्तर देखें37. वृत्त के किसी बिन्दु परखींची गई स्पर्श रेखा और उस बिन्दु से जाने वाली त्रिज्या के बीच का कोण होता है –
A) 45° B) 60° C) 90° D) 120° उत्तर देखें38. दी गई आकृति में, \(TP\) तथा \(TQ\) दो स्पर्श रेखाएँ \(O\) केन्द्र वाले वृत्त पर इस प्रकार हैं कि \(\angle PTQ = 50^\circ\) तो \(\angle POQ =\)
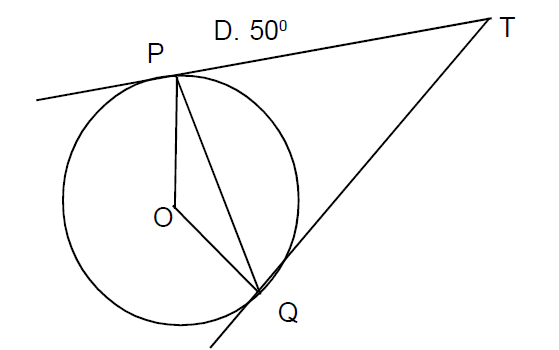 A) 130°
B) 25°
C) 45°
D) 50°
उत्तर देखें
A) 130°
B) 25°
C) 45°
D) 50°
उत्तर देखें
39. दिए गए समकोण \(\triangle PQR\) में \(\angle PRQ = \theta\), \(PQ = 3\) सेमी तथा \(PR = 6\) सेमी तो \(\theta =\)
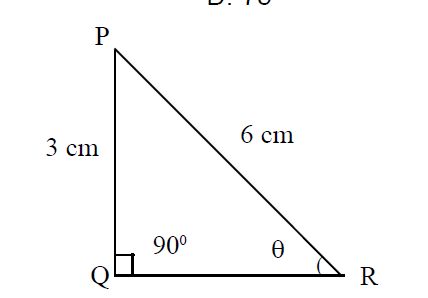 A) 30°
B) 60°
C) 45°
D) 75°
उत्तर देखें
A) 30°
B) 60°
C) 45°
D) 75°
उत्तर देखें
40. यदि \(\tan A = \frac{3}{4}\), तो \(\cos A\) का मान है –
A) \(\frac{3}{5}\) B) \(\frac{4}{5}\) C) \(\frac{5}{4}\) D) \(\frac{5}{3}\) उत्तर देखें41. \(\frac{\cot 44^\circ}{\tan 46^\circ} =\)
A) \(\frac{1}{2}\) B) 0 C) -1 D) 1 उत्तर देखें42. निम्नलिखित में किसका मान सबसे अधिक है?
A) \(\tan 45^\circ\) B) \(\sin 45^\circ\) C) \(\sin 30^\circ\) D) \(\cos 90^\circ\) उत्तर देखें43. यदि एक वृत्त का परिधि 88 सेमी है तो इसकी त्रिज्या है –
A) 7 सेमी B) 14 सेमी C) 21 सेमी D) 28 सेमी उत्तर देखें44. यदि \(\triangle PQR\), \(R\) पर समकोण है, तो \(\sin(P + Q)\) का मान है –
A) 0 B) 1 C) -1 D) \(\frac{1}{3}\) उत्तर देखें45. यदि \(\frac{\alpha}{4} = 15^\circ\) तो \(\sqrt{3} cosec \alpha =\)
A) \(\frac{\sqrt{3}}{2}\) B) 2 C) 3 D) \(\frac{1}{3}\) उत्तर देखें46. यदि \(r_1\) तथा \(r_2\) त्रिज्याओं वाले दो वृत्तों के क्षेत्रों का योग, \(r\) त्रिज्या वाले वृत्त के क्षेत्रफल के बराबर हों, तो –
A) \(r = r_1 + r_2\) B) \(r_1^2 + r_2^2 < r^2\) C) \(r_1^2 + r_2^2 = r^2\) D) \(r_1 + r_2 < r\) उत्तर देखें47. \(\sin (90^\circ – A) =\)
A) \(\sin A\) B) \(\tan A\) C) \(\sec A\) D) \(\cos A\) उत्तर देखें48. एक 15 मीटर लंबी सीढ़ी एक ऊर्ध्वाधर दीवार के शीर्ष तक पहुँचती है। यदि सीढ़ी दीवार के साथ \(60^\circ \) का कोण बनाती है, तो दीवार की ऊँचाई है –
A) 15 मीटर B) 7.5 मीटर C) 5 मीटर D) 30 मीटर उत्तर देखें49. \(\cot 10^\circ \cdot \cot 89^\circ\) का मान है –
A) 1 B) 0 C) 2 D) \(\frac{1}{2}\) उत्तर देखें50. \(r\) त्रिज्या वाले गोला के सम्पूर्ण पृष्ठ का क्षेत्रफल होता है –
A) \(\pi r^2\) वर्ग इकाई B) \(2\pi r^2\) वर्ग इकाई C) \(3\pi r^2\) वर्ग इकाई D) \(4\pi r^2\) वर्ग इकाई उत्तर देखें51. यदि 6, 8, 9, \(x\) तथा 13 का माध्य 10 हो, तो \(x\) का मान होगा –
A) 13 B) 12 C) 15 D) 14 उत्तर देखें52. यदि शंकु की ऊँचाई और त्रिज्या दोगुनी हो जाती है, तो शंकु का आयतन हो जाएगा –
A) 2 गुना B) 4 गुना C) 6 गुना D) 8 गुना उत्तर देखें53. निम्नलिखित वितरण के लिए –
| वर्ग-अंतराल | 0–5 | 5–10 | 10–15 | 15–20 | 20–25 |
|---|---|---|---|---|---|
| बारंबारता | 12 | 17 | 14 | 22 | 11 |
बहुलक वर्ग का निम्न-सीमा है –
A) 15 B) 22 C) 20 D) 35 उत्तर देखें54. निम्नलिखित में से कौन-सा आलेख द्वारा निर्धारित नहीं किया जा सकता है?
A) माध्य B) माध्यक C) बहुलक D) इनमें से कोई नहीं उत्तर देखें55. दो घनों के आयतनों का अनुपात 1 : 27 में है, तो उनकी कोरों का अनुपात है –
A) 1 : 9 B) 9 : 1 C) 1 : 3 D) 3 : 1 उत्तर देखें56. यदि \(\tan \theta = 1\) तो \(\theta\) का मान होगा –
A) 30° B) 45° C) 90° D) 60° उत्तर देखें57. \(x\) भुजा वाली समबाहु त्रिभुज का क्षेत्रफल है –
A) \(x^2\) वर्ग इकाई B) \(\frac{\sqrt{3}}{4}x^2\) वर्ग इकाई C) \(\frac{\sqrt{3}}{2} x^2\) वर्ग इकाई D) \(\frac{\sqrt{3}}{4} x\) वर्ग इकाई उत्तर देखें58. 52 ताश के पत्तों की एक गड्डी को अच्छी तरह फेंटकर उसमें से यादृच्छया एक पत्ता निकाला जाता है। इसके रानी आने की प्रायिकता है –
A) \(\frac{1}{26}\) B) \(\frac{2}{39}\) C) \(\frac{5}{39}\) D) \(\frac{1}{13}\) उत्तर देखें59. यदि \(P(E) = 0.08\) तो \(P(E’)\) बराबर है –
A) 0.92 B) 0.02 C) 0.08 D) 0.52 उत्तर देखें60. \(\frac{1 + \tan^2 \theta}{1 + \cot^2 \theta} =\)
A) \(\tan^2 \theta\) B) \(\sec^2 \theta\) C) \(\cot^2 \theta\) D) -1 उत्तर देखें61. \(0.5 =\)
A) \(\frac{5}{9}\) B) \(\frac{1}{2}\) C) \(\frac{5}{90}\) D) \(\frac{5}{3}\) उत्तर देखें62. बहुपद \(2x^2 + 5x – 12\) का घात है –
A) 1 B) 2 C) 0 D) 3 उत्तर देखें63. \(\sqrt{7}\) है –
A) एक परिमेय संख्या B) एक अपरिमेय संख्या C) एक प्राकृतिक संख्या D) इनमें से कोई नहीं उत्तर देखें64. \(x(x^2 + 2x) =\)
A) \(x^3 + 2x^2\) B) \(x^2 + 2x\) C) \(x^3\) D) \(1 + 2x^2\) उत्तर देखें65. 28 तथा 72 का म0 स0 है –
A) 28 B) 1 C) 4 D) 2 उत्तर देखें66. बहुपद \(x^2 – x + 1\) के शून्यकों का योग होगा –
A) 1 B) -1 C) 0 D) 2 उत्तर देखें67. \((\sqrt{2})^2 – 2 =\)
A) \(\sqrt{2}\) B) 0 C) 2 D) \(2\sqrt{2}\) उत्तर देखें68. \(x + y = 3\) तथा \(3x – 2y = 4\) के हल हैं –
A) \(x = 2, y = 1\) B) \(x = 1, y = 2\) C) \(x = -1, y = 4\) D) \(x = -1, y = -2\) उत्तर देखें69. यदि बहुपद \(y^2 – y – 6\) के शून्यक \(\alpha\) तथा \(\beta\) हों, तो \(\alpha \beta =\)
A) 6 B) -6 C) 1 D) -1 उत्तर देखें70. द्विघात समीकरण \(x^2 – 5x – 300 = 0\) का विविक्तकर होगा –
A) 1225 B) 1500 C) -1225 D) 1325 उत्तर देखें71. समांतर श्रेणी \(\sqrt{18}\), \(\sqrt{50}\), \(\sqrt{98}\), \(\sqrt{162}\) …….. का सार्वंतर है –
A) 2 B) 2\(\sqrt{2}\) C) 3 D) 2\(\sqrt{3}\) उत्तर देखें72. यदि \( y^2 + \frac{1}{y^2} = 14 \) तो \( y + \frac{1}{y} = \)
A) 16 B) 12 C) 8 D) \(+4\) उत्तर देखें73. यदि समांतर श्रेणी का nवाँ पद \(6n – 2\) हो, तो पहला पद होगा –
A) 2 B) 4 C) -2 D) 10 उत्तर देखें74. बिंदु \((-6, 10)\) का कोटि है –
A) -6 B) 10 C) 4 D) -16 उत्तर देखें75. \(\sec^2 A – \tan^2 A =\)
A) 0 B) 1 C) -1 D) 2 उत्तर देखें76. यदि \( x, y, z \) समांतर श्रेणी में हैं तो \( y = \)
A) \(\frac{z – x}{2}\) B) \(\frac{z + x}{2}\) C) \(x + z\) D) \(\frac{x + z}{3}\) उत्तर देखें77. \(\sin A \times \csc A = \)
A) 1 B) 0 C) -1 D) 2 उत्तर देखें78. बिंदुओं \( A(6, 0) \), \( B(14, 0) \) तथा \( C(16, 8) \) से बने त्रिभुज का क्षेत्रफल है –
A) 32 वर्ग इकाई B) 16 वर्ग इकाई C) 44 वर्ग इकाई D) 64 वर्ग इकाई उत्तर देखें79. \(\cot (90^\circ – \theta) =\)
A) \(\cot \theta\) B) \(\tan \theta\) C) \(\csc \theta\) D) \(\sec \theta\) उत्तर देखें80. त्रिभुज के शीर्शों के निर्देशांक \((x_1, y_1), (x_2, y_2)\) तथा \((x_3, y_3)\) हैं, तो केन्द्रक के निर्देशांक हैं –
A) \(\left( \frac{x_1 + x_2 + x_3}{2}, \frac{y_1 + y_2 + y_3}{2} \right)\) B) \(\left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right)\) C) \(\left( \frac{x_1 – x_2 – x_3}{3}, \frac{y_1 – y_2 – y_3}{3} \right)\) D) \( x_1 + x_2 + x_3, y_1 + y_2 + y_3 \) उत्तर देखें81. \(\sin 20^\circ – \cos 70^\circ =\)
A) 1 B) 0 C) 2\( \sin 20^\circ \) D) 2\( \cos 70^\circ \) उत्तर देखें82. \(1 – \cos^4A =\)
A) \(\sin^2A (1 + \sin^2A)\) B) \(\sin^2A (1 – \sin^2A)\) C) \(\cos^2A (1 – \cos^2A)\) D) \(\sin^2A (1 + \cos^2A)\) उत्तर देखें83. यदि \(\sqrt{2} \cos \theta = 1 \) तो \(\theta \) का मान है –
A) 30^\circ B) 45^\circ C) 60^\circ D) 90^\circ उत्तर देखें84. यदि \(\tan \theta = \frac{p}{q} \) तो \(\frac{\cos \theta + \sin \theta}{\cos \theta – \sin \theta} = \)
A) \(\frac{p + q}{p – q}\) B) \(\frac{q + p}{q – p}\) C) \(\frac{q – p}{q + p}\) D) \(\frac{p – q}{p + q}\) उत्तर देखें85. यदि \(\sec A = \frac{25}{7}\) तो \(\sin A =\)
A) \(\frac{24}{25}\) B) \(\frac{7}{24}\) C) \(\frac{7}{25}\) D) \(\frac{25}{24}\) उत्तर देखें86. \(\tan^2 45^\circ – 1 =\)
A) 1 B) 0 C) -1 D) \(\frac{1}{2}\) उत्तर देखें87. \(\frac{1 + \tan^2 A}{\sec^2 A} =\)
A) \(\sin^2 A\) B) 0 C) 1 D) -1 उत्तर देखें88. \(\Delta ABC\) में बिंदु \(D\) और \(E\) क्रमशः भुजाओं \(AB\) तथा \(AC\) पर इस प्रकार हैं कि \(DE \parallel BC\) । यदि \(\frac{AD}{DB} = \frac{4}{5}\) और \(AC = 18\) सेमी तो \(AE =\)
A) 6 सेमी B) 8 सेमी C) 10 सेमी D) 12 सेमी उत्तर देखें89. एक न्यायसंगत पासा फेंका गया तो एक ऋण संख्या आने की प्रायिकता होगी –
A) 1 B) \(\frac{1}{2}\) C) \(\frac{1}{3}\) D) \(\frac{1}{4}\) उत्तर देखें90. यदि दो वृत्तों के क्षेत्रफलों का अनुपात 4 : 25 है, तो उनकी त्रिज्याओं का अनुपात होगा–
A) 3 : 5 B) 5 : 2 C) 1 : 5 D) 2 : 5 उत्तर देखें91. अच्छी प्रकार से फेंटी गई एक ताश की गड्डी में से एक पत्ता यादृच्छय निकाल जाता है, तो इसके लाल रंग का तस्वीर वाला पत्ता होने की प्रायिकता है –
A) \(\frac{1}{26}\) B) \(\frac{2}{13}\) C) \(\frac{3}{13}\) D) \(\frac{3}{26}\) उत्तर देखें92. यदि किसी बंटन का माध्य और माध्यक क्रमश: 4.6 तथा 4.8 है, तो बहुलक =
A) 5 B) 5.1 C) 5.2 D) 5.3 उत्तर देखें93. प्रेक्षण 8, 12, 7, 14, 6, 13, 15 का माध्यक होगा –
A) 9 B) 10 C) 11 D) 12 उत्तर देखें94. माध्यक का तीन गुना और माध्य का दोगुना का अन्तर बराबर होता है –
A) माध्य B) माध्यक C) बहुलक D) इनमें से कोई नहीं उत्तर देखें95. एक घड़ी के मिनट वाली सुई द्वारा 1 मिनट में बनाया गया कोण होता है –
A) 30o B) 15o C) 12o D) 6o उत्तर देखें96. आधार की त्रिज्या \(\textit{r}\) तथा ऊँचाई \(\textit{h}\) वाले एक लंबवृत्तीय बेलन का आयतन होगा –
A) \(\frac{1}{3} \pi r^2 h\) घन इकाई B) \(\frac{2}{3} \pi r^2 h\) घन इकाई C) \(\frac{1}{3} \pi r^2 h^2\) घन इकाई D) \(\pi r^2 h\) घन इकाई उत्तर देखें97. समबाहु त्रिभुज ABC में, यदि AD \(\perp\) BC तो AD\(^2\) =
A) 3CD\(^2\) B) 4CD\(^2\) C) \(\frac{3}{2}\)DC\(^2\) D) CD\(^2\) उत्तर देखें98. त्रिज्या \(r\) वाले अर्धवृत्त का वक्रपृष्ठीय क्षेत्रफल है –
A) \(\pi r^2\) वर्ग इकाई B) \(\frac{\pi r^2}{2}\) वर्ग इकाई C) \(2 \pi r^2\) वर्ग इकाई D) \(3 \pi r^2\) वर्ग इकाई उत्तर देखें99. दी गई आकृति में, O वृत्त का केन्द्र है तथा \(\angle AOC = 130^\circ\) तो \(\angle OAC = \)
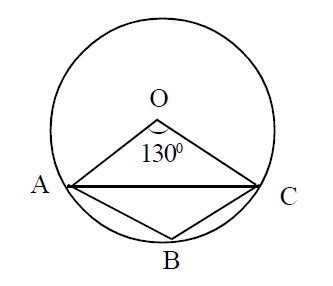 A) 65o
B) 50o
C) 130o
D) इनमें कोई नहीं
उत्तर देखें
A) 65o
B) 50o
C) 130o
D) इनमें कोई नहीं
उत्तर देखें
100. 14 का मिलान चिन्ह है –
A) XIV B)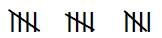 C)
C) 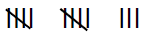 D)
D)  उत्तर देखें
उत्तर देखें
Class 10th math model paper
गणित के मॉडल पपेर (math model paper 2025 Set 4) मे आप को मिलता है सभी chapter से निकले गए गणित महत्वपूर्ण ऑब्जेक्टिव प्रश्न (Important Objective Question) इस मॉडल पेपर को ध्यान से पढने के बाद आप का के 10 से 20 अंक पक्के है और हम कुल 5 मॉडल पेपर(Model Paper) जारी करने वाले है अगर आप ने सभी मॉडल सेट को पढ़ लिया और उसका प्रैक्टिस(practice) कर लिया तो 50 मे 48 पक्के है इस मॉडल पेपर मे
- वास्तविक संख्याएं
- त्रिकोणमिती
- निर्देशांक ज्यामिति
- त्रिभुज
- बहुपद आदि
इन सभी टॉपिक से महत्वपूर्ण ऑब्जेक्टिव प्रश्न (most important objective question) निकले गए है आप के परीक्षा के दृष्टी से और उसको क्विज और मॉडल पेपर मे तैयार किया गया है आप के आसानी के लिए मंतु सर ने चुन चुन कर महत्वपूर्ण प्रश्न निकले है
Bihar Board Class 10th math model paper 2025
हमारे DLS Education के द्वारा तैयार किये गणित Model Paper और Quiz को हल करने से आप अपनी तैयारी का आकलन कर सकते हैं और अपने कमजोर बिंदुओं को सुधार सकते हैं।
सभी वीडियो (YouTube Videos) Click Here
ऑनलाइन तैयारी और अच्छे अंक प्राप्त करें
Mantu Sir ऑनलाइन तैयारी के लिए महत्वपूर्ण मॉडल पेपर (model paper)और Quiz प्रदान कर रहे है और करेंगे ताकि आप परीक्षा (Class 10th Exam 2025) मे अच्छे अंक प्राप्त कर सकें। हमारे कई छात्र हमारे Model paper के माध्यम से अच्छे अंक प्राप्त कर रहे हैं और आप भी इस अवसर का लाभ उठा सकते हैं। बिलकुल मुफ्त

